Дата и время публикации:
Алгоритм и реализация
1. Что это такое
Односвязный, однонаправленный список (singly linked list) используется для объединения, т.е связывания, разобщенных кусков (или элементов) данных в линейную последовательность, размещая их друг за другом и связывая каждый предыдущий с последующим, как показано на рисунке 1.
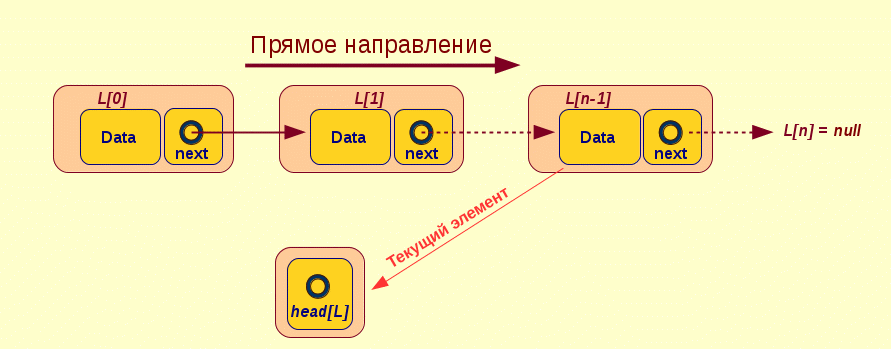
Рисунок 1
/* 4*/ struct __single_llist {
/* 5*/ struct __single_llist *next; /* указывает на следующий элемент или на конец списка NULL */
/* 7*/ void* data; /* указатель на блок данных или другой указатель на функцию или блок данных */
/* 8*/ size_t size; /* содержит размер данных или 0, когда вместо данных был использован указатель */
/* 9*/
/* 10*/ }__attribute__((packed));
/* 11*/
Для сокращение записи введен синоним или спецификатор single_ll_t с использованием ключевого слова typedef, как показано в листинге 1.2
Листинг 1.2. Фрагмент кода из algthm_single_ll.c, проекта gasrunparts, версии 0.7
/* 11*/ /* 12*/ typedef struct __single_llist single_ll_t; /* 13*/
2. Приготовление
Рецепт приготовления однонаправленного списка $L_n$ достаточно прост, потому что в нем четко определены границы – первого $L_0$ и последнего $L_n$, которым является нулевой указатель null, нужный для определения конца списка при "переборе" элементов при помощи указателя next, который обеспечивает "пролистывание" элементов в прямом направлении согласно алгоритму 2.1 .
Алгоритм 2.1
\(SLLIST \_ ITEM \_ FORWORD(L)\)
\(head[L] \leftarrow next[x \leftarrow head[L]]\)
\(\mathbf{return} \ head[L]\)
Процедура SLLIST_ITEM_FORWORD(L) будет возвращать элемент \(head[x \leftarrow next(x)]\) из списка $L$ за время, равное асимптотической оценки O(1), которое несравнимо со временем работы O(n), как будет показано ниже в алгоритме 2.2.
В нем, осуществляется добавление нового элемента $х$ в конец списка $L$ путем предварительного пролистывания элементов с первого и до последнего.
Алгоритм 2.2
\(SLLIST \_ ITEM \_ APPEND(L,x)\)
\(head[L] \ \leftarrow \ L[0]\)
\(\mathbf{While} \ head[L] != NIL\)
\(\mathbf{do}\)
\(prev \ \leftarrow \ head[L]\)
\(head[L] \leftarrow next[prev]\)
\(\mathbf{if} \ x \ \neq \ NIL\)
\(\mathbf{then}\)
\(head[L] \ \leftarrow \ x\)
\(\mathbf{if} \ prev \neq \ NIL \)
\(\mathbf{then}\)
\( next[prev] \ \leftarrow \ head[L]\)
\( head[L] \ \leftarrow \ L[0]\)
\(\mathbf{return} \ head[L] \)
Перед добавлением элемента $x$ смещаемся на последний элемент списка $L$, затратив для этого время, равное асимптотической оценки O(n) по числу элементов в нем. Затем, после этого добавляем новый элемент $x$, делаем его текущим и возвращаем указатель $head[L]$ в качестве указателя на текущую позицию в списке $L$.
/* 53*/ #define SINGLE_LLIST_ITEM_APPEND(L,x) ({ \
/* 54*/ single_ll_t *__head = (L), *__x = (x), *__prev=NULL; \
/* 55*/ if ( x ) \
/* 56*/ do{ \
/* 57*/ for ( ; (__head) ; (__head)= (__prev)->next ) \
/* 58*/ (__prev) = (__head); \
/* 59*/ if ( (__x) ) { \
/* 60*/ (__head) = (__x); \
/* 61*/ if ( (__prev) ) (__prev)->next = (__head); \
/* 62*/ } \
/* 63*/ }while(0); __head; })
Так как SINGLE_LLIST_ITEM_APPEND(L,x) возвращает указатель на крайний элемент, поэтому нужно чиркануть функцию, которая не позволит потерять "начало" списка для дальнейших операций с ним, как показано в листинге 2.2.2
Листинг 2.2.2. Фрагмент кода из algthm_single_ll.c, проекта gasrunparts, версии 0.7
/* 67*/ static __inline__ single_ll_t *single_llist_item_append ( single_ll_t *list_p, single_ll_t *x_p )
/* 68*/ {
/* 69*/ single_ll_t *head_p = SINGLE_LLIST_ITEM_APPEND(list_p,x_p);
/* 70*/ return ( !list_p ? head_p : list_p );
/* 71*/ }
Напротив, алгоритм 2.3 отличается элегантностью, простой и не требует затрат по времени.
Алгоритм 2.3
\(SLLIST_ITEM_PUSH(L,x)\)
\(head[L] \ \leftarrow \ L[0]\)
\(\mathbf{if} \ x \neq NIL\)
\(\mathbf{then}\)
\(next[х] \leftarrow head[L]\)
\(head[L] \leftarrow x\)
\(\mathbf{return} \ head[L]\)
\(\mathbf{return} \ NIL \)
Где вставка элемента $x$ осуществляется в начале списка, перед элементом $L[0]$.
Таким образом, отсутствует необходимость усложнять алгоритм постоянным поиском конечного элемента в момент вставки, а время работы сокращается с O(n) до O(1).
/* 79*/ #define SINGLE_LLIST_ITEM_PUSH(L,x) ({ \
/* 80*/ single_ll_t *__head = (L), *__x = (x); \
/* 81*/ if ( (__x) ) { \
/* 82*/ (__x)->next = (__head); \
/* 83*/ (__head) = (__x); \
/* 84*/ } \
/* 85*/ __head; })
Следовательно, удаление элементов $L_n$ из списка так же разумно производить не с хвоста, а с головы, последовательно удаляя каждый элемент $L_i$, как показано в алгоритме 2.4.
Алгоритм 2.4
\(SLLIST \_ ITEM \_ POP(L)\)
\(x \ \leftarrow \ L[0] \)
\(\mathbf{if} \ x \neq \ NIL \)
\(\mathbf{then}\)
\(head[L] \ \leftarrow \ next[x]\)
\(\mathbf{return} \ x \)
Если указатель на элемент $L[0]$ является не нулевым, производим его удаление, т.е. выталкиваем из списка, а начало сдвигаем на элемент $L[1]$.
/* 71*/ static __inline__ single_ll_t *single_llist_item_pop(single_ll_t ** list_pp) {
/* 72*/ single_ll_t *item_p = ( list_pp ? *list_pp : NULL );
/* 73*/ if( item_p ) {
/* 74*/ *list_pp = item_p->next;
/* 75*/ }
/* 76*/ return item_p;
/* 77*/ }
В то же время от асимптотической оценки, равной О(n), ни куда не уйти, особенно при решении таких задач, как достижение конца списка $L_n$, приведенной в алгоритме 2.5.
Алгоритм 2.5
\(SLLIST \_ DEPTH(L) \)
\(n \ \leftarrow \ 0 \)
\(head[L] \ \leftarrow \ L[0] \)
\(\mathbf{while} \ head[L] \neq \ null \ \)
\(\mathbf{do}\)
\(n \ \leftarrow \ n \ + \ 1\)
\(head[L] \ \leftarrow \ next[head[L]]\)
\(\mathbf{return} \ n \)
/* 87*/ #define SINGLE_LLIST_DEPTH(L) ({ \
/* 88*/ single_ll_t *__head = (L); size_t __n = 0; \
/* 89*/ do{ \
/* 90*/ while ( (__head) != NULL ) { (__head) = (__head)->next; (__n)++; } \
/* 91*/ }while(0); __n; })
/* 92*/
Данный оператор-выражениe достигает конца списка в строке 90, когда элемент $L_i$ становится равен конечному элементу $L_n$ или null согласно рисунку 1.
При этом, как наглядно показано на рисунке 3.1, асимптотическая оценка О(n) легко может превратиться в $О(n^2)$, если доступ к элементам списка $L_n$ осуществляется последовательным пролистыванием, как показано в листинге 2.6
Алгоритм 2.6
\(SINGLE \_ LLIST \_ ITEM \_ GET(L,idx)\)
\(n \ \leftarrow \ 0 \)
\(head[L] \ \leftarrow \ L[0] \)
\(\mathbf{while} \ head[L] \neq \ NIL \)
\(\mathbf{do}\)
\(\mathbf{if} \ n = idx\)
\(\mathbf{then}\)
\(\mathbf{return} \ head[L]\)
\(n \ \leftarrow \ n \ + \ 1\)
\(head[L] \ \leftarrow \ next[head[L]]\)
\(\mathbf{return} \ NIL\)
/* 93*/ #define SINGLE_LLIST_ITEM_GET(L,idx) ({ \
/* 94*/ single_ll_t *__head = (L); \
/* 95*/ unsigned long __idx = (idx), __n = 0; \
/* 96*/ do{ \
/* 97*/ for ( ; (__head) ; (__head)=(__head)->next ) \
/* 98*/ if ( (__idx) == (__n)++ ) break; \
/* 99*/ }while(0); __head; })
/*...*/
/*278*/ for ( nitems=100UL; nitems < 2100; nitems += 100 ) {
/*279*/ (void)test_procedure_for_four_stage( nitems, &tm_stat );
/*...*/
/*284*/ }
/*...*/
/*291*/ static int test_procedure_for_four_stage( unsigned long nitems,
/*292*/ timer_stat_t *tm_stat_p )
/*293*/ {
/*...*/
/*318*/ for ( item_i=0 ; item_i < nitems; item_i++ ) {
/*...*/
/*321*/ item_p = SINGLE_LLIST_ITEM_GET(list_p,idx);
/*...*/
/*330*/ }
/*...*/
/*357*/ }
При этом, как вытекает из строки 318 рассматриваемого листинга, при циклических манипуляциях с оператором-выражением SINGLE_LLIST_ITEM_GET(), асимптотическая оценка вырастет с $О(n^2)$ до $О(n)$, что наглядно иллюстрирует рисунок 3.1
3. Ограничения и рекомендации
1. Исходя из асимптотической оценки алгоритмов 2.2 и 2.5, равной О(n), следует, что добавление и удаление элементов из односвязного списка, вмещающего элементов $L_n$, где $n \rightarrow $ ∞, чревато большими тормозами и задержками при использование метода пролистывания (Serial access) с данными большого объема. Поэтому метод выталкивания первого элемента (POP method), вытекающий из схемы FIFO: первым пришел – первым ушел, показанной в алгоритмах 2.3 и 2.4, является оптимальным при интенсивном обмене данных.
2. В тоже время, для оптимизации времени доступа к элементам списка $L$, начиная с $L[2]$ и заканчивая $L[n-1]$, лучше производить с использованием хэш-таблицы с прямой адресацией(Hash table) и некоторых расширений GCC. При этом нужно помнить, что любой из перечисленных способов доступа к элементу списка $L_i$ не всегда дает ощутимых преимуществ, когда список содержит небольшое число элементов, например менее 100, как показано на рисунке 3.1
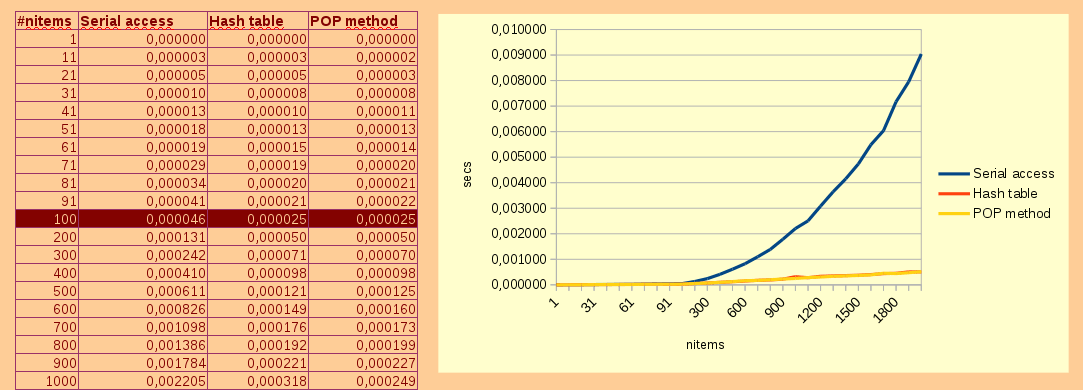
Рисунок 3.1
2. Поэтому, согласно приведенным данным на рисунке 3.1, выигрыш от использования метода POP и hash table по сравнению с Serial access начинает наблюдаться на списках, число элементов которых переваливает за 100. При этом надо отметить, что первый метод удаляет элемент из списка в чем не всегда есть надобность, что делает метод hash table более предпочтительным в операциях произвольного доступа к элементу списка несмотря на небольшой проигрыш по времени перед методом POP.
3. Эффективность метода hash table кроется в алгоритме 3.1, где приведена вставка или вернее добавление ключей в хэш-таблицу.
Алгоритм 3.1
\( DIRECT \_ HASH \_ INSERT(H,х)\)
\(H[key[x]] \ \leftarrow \ x\)
Хэш-таблицы с прямой адресацией по ключу $key[x]$ являются индиксируемым, однородным массивом $H$ из указателей, содержащие адреса элементов списка $L_n$, по значению которых можно рассчитать ключ при условии однородности данных по типу и размеру.
В нашем случае, когда данные неоднородны и элементы списка $L_n$ могут быть перемешаны с другими данными, не имеющие отношение к списку $L$, тогда наступает частный случай DIRECT_HASH_INSERT(H,х), реализуемый алгоритмом 3.2
Алгоритм 3.2
\(SLLIST \_ DIRECT \_ HASH \_ INSERT(H,x)\)
\(\mathbf{if} \ x \neq NIL\)
\(\mathbf{then}\)
\(key[x] \ \leftarrow \ length[H]\)
\(H[key[x]] \ \leftarrow \ x\)
\(\mathbf{return} \ length[H]\)
Для элемента, а вернее адреса $x$, значение ключа $key[x]$ вычисляется по текущей длине хэш-таблицы $length[H]$, что неизбежно приведет выхода за её границы. Таким образом, перед присвоением адреса $x$ элементу $H[key[x]]$, необходимо выполнить процедуру выделения памяти.
/*103*/ struct __sll_hash_table {
/*104*/ single_ll_t** table_p;
/*105*/ __usize_t length;
/*106*/ };
/*107*/
/*108*/ typedef struct __sll_hash_table sll_hash_tbl_t;
/*109*/
/*110*/ #define hash_table hash_tbl_p->table_p
/*111*/ #define hash_length hash_tbl_p->length
/*112*/
В строке 104 объявлен двойной указатель на массив хэш-таблицы, состоящей из указателей элементов списка $L_n$, и добавляемых в момент вызова встраиваемой функции sll_hash_tbl_insert(), которая осуществляет вставку в конец хэш-таблицы нового адреса с предварительным выделением под него памяти и увеличение length на 1, как показано в листинге 3.2.2.
Листинг 3.2.2. Фрагмент кода из algthm_single_ll.c, проекта gasrunparts, версии 0.7
/*122*/ static __inline__ int sll_hash_tbl_insert ( sll_hash_tbl_t *hash_tbl_p, single_ll_t *head )
/*123*/ {
/*124*/ if ( hash_tbl_p && head ) {
/*125*/ hash_table = (single_ll_t **)( hash_table != NULL ?
/*130*/ realloc ( hash_table, (hash_length+1) * sizeof(single_ll_t*) ) :
/*131*/ malloc ( sizeof(single_ll_t*) ) );
/*128*/ if ( hash_table ) {
/*129*/ *(hash_table+hash_length) = head;
/*130*/ hash_length++;
/*131*/ return 0;
/*132*/ }
/*133*/ }
/*134*/ return -1;
/*135*/ }
В строках 125-131 осуществляется выделение памяти, а в строках 129 и 130 вставку в конец хэш-таблицы нового адреса и увеличение длинны таблицы length на 1.
Так же алгоритм 3.2 в чем-то повторяется при реализации произвольного доступа к элементу списка $L_i$ c использованием хэш-таблицы, как показано в листинге 3.3
Алгоритм 3.3
\(SLLIST \_ DIRECT \_ HASH \_ GET(H,idx)\)
\(\mathbf{if} \ H \neq NIL \land idx \lt length[H] \)
\(\mathbf{then}\)
\(key[x] \ \leftarrow \ idx\)
\(\mathbf{return} \ H[key[x]]\)
\(\mathbf{return} \ NIL\)
/*137*/ static __inline__ single_ll_t* sll_hash_tbl_get ( sll_hash_tbl_t *hash_tbl_p, unsigned long idx )
/*138*/ {
/*139*/ return ( hash_tbl_p == NULL ? NULL :
/*140*/ (idx < hash_length ? *(hash_table+idx) : NULL) );
/*141*/ }
При этом, значением ключа $key[х]$ является idx, принятый в строке 137.
Следовательно, как вытекает из алгоритма 3.2 и 3.3 использование таблицы хеширования с прямой адресацией позволяет сохранить общую асимптотическую оценку $O(n)$ для произвольного доступа к одно- связному и направленному списку $L_n$. Учитывая, что при благоприятном стечении звезд время обращения к одному элементу будет равно $O(1)$ и не более. В противовес плохому сценарию, который реализуется произвольным доступом к $N$-элементам списка $L_n$ с последовательным пролистыванием, время выполнения алгоритма уже составит $O(n^2)$.
4. Библиография