Дата и время публикации:
Определение и использование
1. Что это такое
Нотации Θ-, О- или Ω-большое используются в вычислительной технике для оценки сложности и быстродействия алгоритмов, а именно времени, которое требуется на отработку заложенного программистом сценария или, к примеру, сколько нужно ему памяти в ОЗУ или объема накопителя информации. При этом, так называемая скорость роста времени работы алгоритма растет не только из-за его сложности, используемой техники языка программирования или быстродействия вычислительной машины, но и с размером ввода. Поэтому, как говорит один мой знакомый кролик – это не только ценный мех, но и 5 кг мяса, о которых речь пойдет дальше.
2. Функция роста времени выполнения
Любой алгоритм растет по-мере подачи на вход данных, размером $n \ \rightarrow $ ∞, в соответствие с требуемым времени их обработки и числа машинных команд(они же – инструкции). Поэтому чем витиеватей и сложен код, тем быстрее будет расти его время выполнения, тенденцию которому задает размер ввода, равный $n$.
Для наглядности рассмотрим фрагмент исходного кода из проекта procps_ptree, который приведен в листинге 1.
Листинг 1. фрагмент кода из файла main.c
/*...*/
/*292*/static int procps_plist_sort ( proc_data_t *pd_p )
/*293*/{
/*294*/ sort_node_t *tmp_list = sort_list;
/*295*/
/*296*/ tmp_list = malloc( sizeof(sort_node_t)); /* ppid */
/*297*/ if ( !tmp_list ) {
/*298*/ return -1;
/*299*/ }
/*300*/ tmp_list->sr = sr_ppid;
/*301*/ tmp_list->next = sort_list; /* 0xdeadbeef */
/*302*/ sort_list = tmp_list;
/*303*/
/*304*/ tmp_list = malloc ( sizeof(sort_node_t) ); /* start_time */
/*305*/ if ( !tmp_list ) {
/*306*/ free( tmp_list );
/*307*/ return -1;
/*308*/ }
/*309*/ tmp_list->sr = sr_start_time;
/*310*/ tmp_list->next = sort_list;
/*311*/ sort_list = tmp_list;
/*312*/
/*313*/ qsort ( pd_p->tab, pd_p->n, sizeof(proc_t*), compare_two_procs );
/*314*/
/*315*/ if ( sort_list->next ) {
/*316*/ free ( sort_list->next );
/*317*/ }
/*318*/ free ( sort_list );
/*319*/
/*320*/ return 0;
/*321*/}
Несмотря на благоприятное влияние звезд и программиста с бубном, выражающееся в мощности вычислительных ресурсов, применяемой техники программирования и размера ввода $n$, рост функции времени выполнения кода $f(n)$ в строках 294-318 – можно описать как
\(f(n) = n^2 + 4n + 1\) инструкций,
потому что в строке c 294 по 311-й повторяется одна и та же последовательность операций присвоения операндов, которая составит $3n$ инструкций, если конечно исключить влияние функции malloc(). В тоже время считаем, что процедура сортировки QSORT(3) в строке 313 занимает $n^2$ инструкций. Оставшийся код, в строках 315-318, будет равен примерно $n + 1$ инструкций. Отсюда, решая простое уравнение $n^2 + 3n + n + 1$ получим \(n^2 + 4n + 1\) инструкций.
На рисунке 1 показана зависимость роста функции $f(n)$ от размера ввода $n$ и её частей – \(n^2\) и \(4n + 1\).
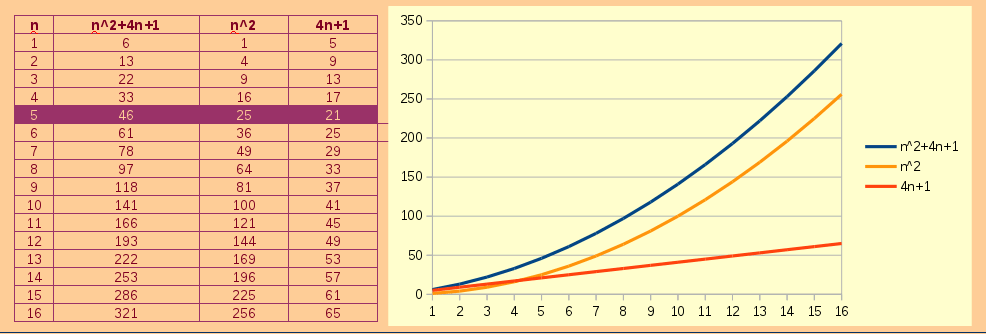
Рисунок 1
Как следует из рисунка 1, компонент $n^2$ растет быстрее чем оставшиеся часть $4n + 1$ функции $f(n)$. При этом, как иллюстрирует на нем график роста нашей функции \(n^2 + 4n + 1\), на её крутизну больше оказывает влияет \($n^2\), а не оставшаяся часть \(4n + 1\), которую можно отбросить при больших значениях $n$.
Таким образом, для времени выполнения $an^2 + bn + с$ и некоторых чисел, а вернее для константных коэффициентов $a \gt 0, b$ и $с$ будут существовать такие значения $n$, при которых $an^2$ будет больше чем $bn + с$, что и следует из нашего случая $1n^2$ больше чем $4n + 1$ при значениях $n \ge 5$. В то же время коэфициент $a=1$ показывает, что на него можно то же не обращать внимание, так как он перестает влиять на крутизну графика $n^2$ при $a \ge \ b+c$.
Поэтому путем отбрасывания менее значищих частей и константных коэффициентов можно сфокусироваться на более важной составляющей – времени выполнения алгоритма, а именно роста его скорости без необходимости вникать в детали не требующие внимания. Соответственно, после отбрасывания шелухи можно получить одну из трех форм асимптотической нотации в виде $\Theta$-большая, O-большая и $\Omega$-большая.
3. Нотация $\Theta$-большая
Самой "энергозатратной", из ранее рассмотренного исходного кода в листинге 1, является библиотечная функция QSORT(3) в строке 313, которая использует функцию обратного вызова compare_two_procs(). Поэтому настало пора взглянуть на эту точку кода более подробно и выявить её причины грехопадения.
Если с библиотечной функцией QSORT(3) все ясно и известна её скорость роста времени выполнения, то с функцией обратного вызова compare_two_procs() не так все просто.
Поэтому найдем функцию $f(n)$ общего времени выполнения compare_two_procs(). Для чего выделим код этой "павшей девки империализма" и распишем всю цепочку шажков наихудшего сценария её жизни.
Листинг 3.1 фрагмент кода из файла main.c, проекта procps_ptree
/*156*/ typedef int (*sr_t)(const proc_t* P, const proc_t* Q);
/*157*/
/*158*/ typedef struct sort_node {
/*159*/
/*160*/ struct sort_node *next;
/*161*/ int (*sr)(const proc_t* P, const proc_t* Q); /* sort function */
/*162*/
/*163*/} sort_node_t;
/*164*/
/*165*/ #define CMP_SMALL(NAME) \
/*165*/ static int sr_ ## NAME (const proc_t* P, const proc_t* Q) { \
/*166*/ return (int)(P->NAME) - (int)(Q->NAME); \
/*167*/ }
/*168*/
/*169*/ #define CMP_INT(NAME) \
/*170*/ static int sr_ ## NAME (const proc_t* P, const proc_t* Q) { \
/*171*/ if (P->NAME < Q->NAME) return -1; \
/*172*/ if (P->NAME > Q->NAME) return 1; \
/*173*/ return 0; \
/*174*/ }
/*...*/
/*183*/ static sort_node_t *sort_list;
/*...*/
/*276*/ CMP_SMALL(ppid);
/*277*/ CMP_INT(start_time);
/*278*/
/*279*/ static int compare_two_procs(const void *a, const void *b ) {
/*280*/
/*281*/ sort_node_t *tmp_list = sort_list;
/*282*/
/*283*/ while ( tmp_list != (sort_node_t *)NULL ) {
/*284*/ int result = (*tmp_list->sr)(*(const proc_t *const*)a, *(const proc_t *const*)b);
/*285*/ if( result ) return result;
/*286*/ tmp_list = tmp_list->next;
/*287*/ }
/*288*/ return 0; /* no conclusion */
/*289*/ }
/*290*/
/*...*/
/*300*/ tmp_list->sr = sr_ppid;
/*...*/
/*309*/ tmp_list->sr = sr_start_time;
/*...*/
/*313*/ qsort ( pd_p->tab, pd_p->n, sizeof(proc_t*), compare_two_procs );
/*...*/
Сделаем первый шажок сбросим шулуху и оставим все важное, потому что помимо двух операций присваивания большую часть времени занимает выполнение цикла while.
Второй шажок, рассчитаем количество вычислений в цикле while, выполняемого в строках 283-287, при наихудшем сценарии, когда сортируются элементы $x_n$ в двумерном pd_p->tab цикл делает $n$ итарраций для проверки всех условий сортировки:
в строке 284 проверяется условие сортировки указанного двумерного массива для элементов $a_i$ и $b_i$. В случае, если возвращается ненулевое значение, тогда выполнение цикла прерывается в строке 285 вместе с выполением функцией compare_two_procs(), а QSORT(3) выполняет сортировку .
В обратном случае, если условие сортировки равно нулю в строке 286 осуществляется переход на следующий элемент в односвязном списке sort_list и так до тех пор, пока в строке 283 не будет достигнут конец списка.
В третьем шажке, находим функцию общего времени выполнения $f(n)$, которая состоит из:
времени выполнения всех итераций $n$ рассматриваемого цикла, равное $С1*n$, где $С1$ – время выполнения одной итерации цикла независяшее от быстродействия вычислительных средств, языка программирования, возможностей в оптимизации исходного кода комилятором и других факторов.
времени выполнения операций присваивания, перечисленных в первом шажке, равное $С2$ и являющееся постоянным.
Таким образом, функция общего времени выполнения $f(n)$ для compare_two_procs() имеет вид:
$f(n)=С1*n+С2$
Но, $f(n)$ не дает представления о скорости роста времени выполнения и, соответственно, не позволяет сделать асимптотическую оценку в виде нотации Θ(n), которой соответствует быстродействие алгоритма compare_two_procs().
Поэтому для алгоритма, который описан функцией $f(n)$ и имеющий $n$ линейных вхождений, всегда будет существовать благоприятный и наухудщий случай, когда $n \rightarrow$ ∞. Следовательно, $f(n)$ сверху и снизу в зависимости тенденции роста $n$ и некоторых коэфициентов $K_1$ (понизу) и $K_2$ (поверху).
Соотвественно, когда говорят, что время выполнения Θ($f(n)$) ограничена c двух сторон, как ветчина в гамбургере, то имеют ввиду, что оно находится между минимальной границей $K_1*f(n)$ и максимальной границей $K_2*f(n)$. Перефразируя сказанное, можно утвержадать, что большая Θ должна быть не хуже, но и не лучше самой функции $f$:
Θ($f(n)$)$ = $O($f(n)$) $ \cap $ Ω($f(n)$),
что в принципе и соблюдается, если обратим свой взор на рисунок 2.
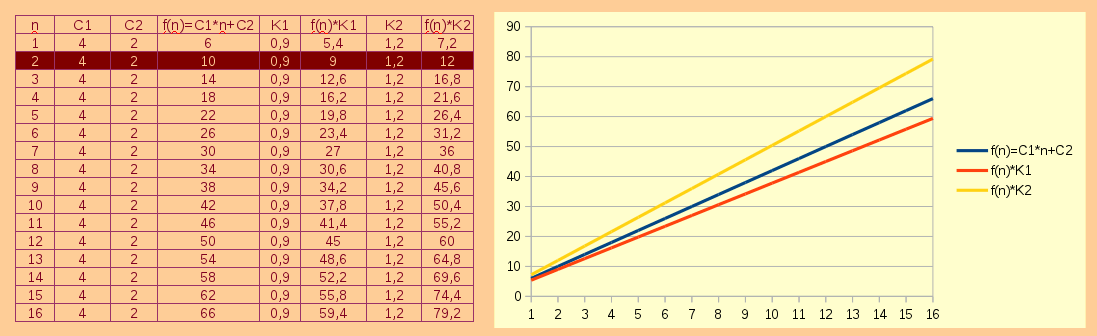
Рисунок 2
Таким образом, нотацию Θ($n$) используют для задания асимптотически "жестких границ" времени выполнения некоторой функции $f$ на больших значениях $n$. Поэтому, если обратимся к рисунку 2, иллюстрирующий рост функции времени выполнения $f(n)$, то увидим, что она имеет две границы асимптотического выравнивания – верхнюю $O(n)$ и нижнюю $\Omega(n)$, которые начинают "играть" при значениях $n \ge 2$, потому что на $n = 1$ функции $f(n)$ соприкасается с нижней границей.
Кроме линейной функций $\Theta(n)$ в нотациях Θ-, О- и Ω-большое могут использоваться следующие, как показано ниже на примере рассматриваемой нотации.
$1. \ Θ(1)$
$2. \ \Theta(\lg n)$
$3. \ \Theta(n \lg n)$
$4. \ \Theta(n^2)$
$5. \ \Theta(n^2 \lg n)$
$6. \ \Theta(n^3)$
$7. \ \Theta(2^n)$
4. Нотация O-большая
В отличие от \(\Theta(f)\), данная нотация применяется для ограничения роста функции $f(n)$ поверху, т.е. когда она стремится к верхней границе \(K_2*f(n)\) на больших значениях $n$
Для примера рассмотрим...
5. Библиография
3) Algorithms for dummies (Part 1): Big-O Notation and Sorting
4) Rob Bell. A beginner's guide to Big O notation
5) Анализ сложности алгоритмов. Примеры